Obwohl sie es eigentlich alle besser wissen müssten, wird die Unsicherheit von Wahlumfragen und Prognosemodellen von vielen Bürgern, Journalisten und Politexperten geflissentlich ignoriert. So lassen sich aus reinen Zufallsschwankungen spannende Nachrichten zu politischen Kopf-an-Kopf-Rennen stricken oder Demoskopen für politische Ausgänge schelten, welcher durchaus innerhalb der üblichen Fehlertoleranz gelegen haben. Damit kann man sich natürlich abfinden. Man kann sich aber auch die Frage stellen, ob wir nicht vielleicht ein Kommunikationsproblem haben und Wege finden sollten, diese Unsicherheit besser zu vermitteln. Am einfachsten wäre das wohl durch geeignete graphische Darstellungen. Wie also sollen wir die Unsicherheit von Wahlumfragen visualisieren? Interessanterweise gibt es bislang relativ wenige empirisch gesicherte Vorschläge dazu, wie dies am besten zu bewerkstelligen wäre (Spiegelhalter et al. 2011).

Ist Unsicherheit nur eine weitere Variable?

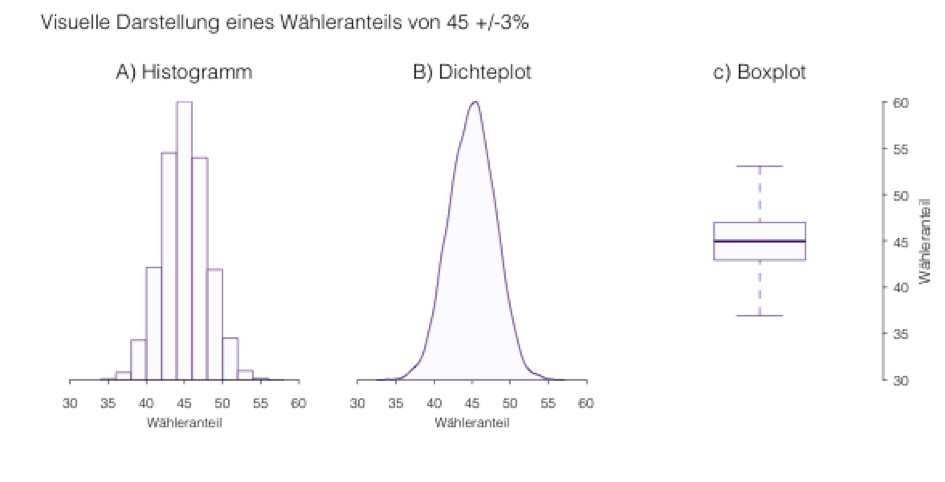
Die erste Frage die sich bei der graphischen Darstellung von statistischer Unsicherheit stellt, ist ob es sich dabei lediglich um eine weitere, wie alle anderen zu visualisierende Variable handelt, oder ob ihr nicht ein gänzlich anderer Status zukommen sollte, der sich auch in neuen Visualisierungsmethoden widerspiegelt. Dies ist eng verbunden mit der Unterscheidung von empirischen Variablenverteilungen und den Verteilungen von Stichprobenkennwerten. Stichproben- und Vorhersageunsicherheit lassen sich beide in Form von Wahrscheinlichkeitsverteilungen beschreiben. Eine Möglichkeit zur Visualisierung von Unsicherheit bestünde dann also ganz einfach darin, graphische Methoden für die Darstellung von uni-variaten empirischen Verteilungen, also Histogramme, Dichteplots oder box plots und deren Verwandten zu verwenden.

Variationen des Error Bars

Wissenschaftler visualisieren Unsicherheit in der Regel, indem sie error bars zu bestehenden Graphikformaten, etwa einem Balkendiagramm, hinzuzufügen. Der Grad der Unsicherheit wird hier durch die Länge einer kleinen Linie illustriert. Die Endpunkte dieser Linien geben entweder den ermittelten Datenpunkt plus/minus den Standardfehler oder die Grenzen des 95%-Konfidenzintervalls an. Allerdings werden Balkendiagramme mit error bars auch kritisiert. Neben der Tatsache, dass selbst Wissenschaftler Schwierigkeiten haben sie zu verstehen und nicht immer klar ist, ob sie sich auf die Fehlertoleranz oder ein Konfidenzintervall beziehen, verleiten sie zu zwei Fehlschlüssen. Erstens, vermitteln sie den Eindruck einer uniformen Wahrscheinlichkeitsverteilung bei der alle Werte innerhalb des error bars gleich wahrscheinlich sind und Werte außerhalb des error bars gar nicht vorkommen. Zweitens, haben Psychologen ermittelt, dass Menschen den Linienabschnitt innerhalb des Balken schlechter wahrnehmen und die darin enthaltenen Werte als wahrscheinlicher betrachten, weil sie vom Balken visuell „eingeschlossen“ sind: der sogenannte within-the-bar-bias.

Natürlich gibt es einige Möglichkeiten, den genannten Problemen zu begegnen. William Cleveland (1994), ein Schwergewicht der Erforschung statistischer Graphiken, rät dazu error bars auf dot plots anzuwenden, um den within-the-bar-bias zu eliminieren. Dies führt dann zu einem Design, das manche Nerds liebevoll als tie fighter plot bezeichnen. Andere Visualisierungsmöglichkeiten bestehen darin, ein Konfidenzband zu verwenden, welches ein Konfidenzintervall nicht als Linie sondern als Flächensegment in hellerer Farbe darstellt. Dies ist etwa die Visualisierungsmethode, welche die Süddeutsche Zeitung vor kurzem für Ihre Balkendiagramme gewählt hat. Die geschätzten Kollegen von zweitstimme.org kombinieren Konfidenzbänder mit dot plots und wählen damit insgesamt wohl keine schlechte Visualisierungsstrategie. (Im Gegensatz zu den Journalisten der SZ interpretieren sie die entsprechenden Wahrscheinlichkeiten auch richtig. Aber das ist ein anderes Thema und soll ein anderes Mal erläutert werden.)

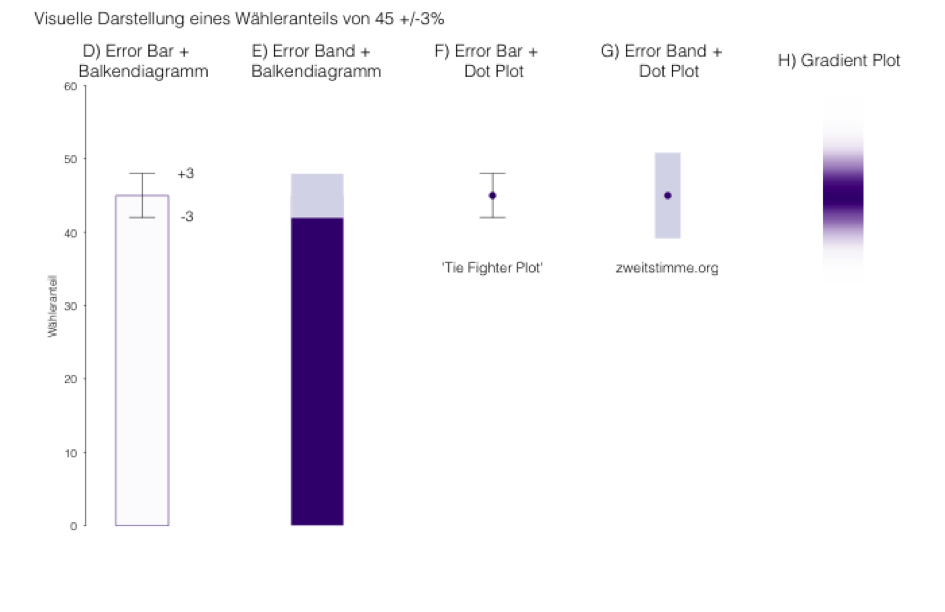
Ist der Gradient Plot eine Lösung?

Ein gänzlich anderer Vorschlag, Unsicherheit zu visualisieren sind gradient plots (Jackson 2008). Die zentrale Idee ist hier die Wahrscheinlichkeitsverteilung durch Farbintensität abzubilden. Es gibt drei Gründe, warum sich diese Visualisierungsmethode als überlegen erweisen könnte. Erstens, gibt der visuelle Stimulus die Verteilung der zugrundliegenden Quantitäten auf intuitive Weise wieder, da dunklere Farben höhere Wahrscheinlichkeiten anzeigen. Zweitens, führt diese kontinuierliche Visualisierungsstrategie mit etwas unpräzisen Rändern dazu, dass Betrachter in ihrer Interpretation vorsichtiger sind, als dies für die diskreten aber sehr präzisen Grenzen eines error bars der Fall wäre. Zuletzt weisen gradient plots eine klare Symmetrie um den Erwartungswert auf und vermeiden somit within-the-bar-bias.

Noch wissen wir zu wenig

Welche empirische Evidenz gibt es für die relativen Vorzüge die Unsicherheit in Wahlumfragen auf die eine oder andere Weise zu visualisieren? Die Computerwissenschaftler Correll und Gleicher (2014) zeigen in einem Experiment, dass das in der Wissenschaft übliche Format des Balkendiagramms mit error bars dem gradient plot unterlegen ist und Menschen mehr Fehler in der Einschätzung von politischen Ergebnissen machen. Zusammen mit meinen Kollegen Lucas Leemann und Felix Jäger konnten wir diesen Befund in unseren eigenen crowd-sourced Experimenten bislang jedoch nicht replizieren. Auch fanden wir keinen Hinweis auf unterschiedliche Verhaltensimplikationen: unterschiedliche visuelle Darstellungen von Unsicherheit verleiten die Menschen nicht in unterschiedlichem Maße dazu, Wetten über politische Wahlausgänge einzugehen. Stattdessen scheinen die bislang unüblichen gradient plots den Beobachter zu verunsichern und das Vertrauen in die eigene Urteilskraft zu senken. Neue Visualisierungsexperimente sind allerdings bereits in Planung und wir sind zuversichtlich, schon bald mehr über die Visualisierung von Unsicherheit von Wahlumfragen zu lernen. Bis zur anstehenden Bundestagswahl müssen wir aber wohl weitere Kommentierungen von random noise über uns ergehen lassen und nach der Wahl haben die Demoskopen bestimmt wieder alles falsch gemacht.

Literaturhinweise

Cleveland, William S. 1994. The Elements of Graphing Data (Revised 2nd Edition). Hobart Press.

Correll, Michael, and Michael Gleicher. 2014. Error bars considered harmful: Exploring alternate encodings for mean and error. IEEE transactions on visualization and computer graphics 20(12): 2142-2151.

Jackson, Christopher H. 2008. Displaying uncertainty with shading. The American Statistician 62(4): 340-347.

Leemann, Lucas und Richard Traunmüller. 2017. Polls, Uncertainty and Perceived Uncertainty of Polls. Paper presented at the ECPR General Conference 2017 in Oslo.

Spiegelhalter, David, Mike Pearson, and Ian Short. 2011. Visualizing uncertainty about the future. Science 333(6048): 1393-1400.